a very occasional diary @ Nikita Danilov
2025-04-23
2025-03-09
Review of Feminism, Interrupted: Disrupting Power by L. Olufemi
Review of Feminism, Interrupted: Disrupting Power by L. Olufemi, Pluto Press, 2020
“feminism means freedom, it means the right to be […] incoherent “, p. 71
Let me state outright, that I won’t be able to provide a critique of the cogent rational argument that forms the core of Ms. Olufemi's book, for the simple fact that even the most diligent search will not find an argument of that sort there.
I am going to prove with ample internal and external evidence, that the book does not present an articulated argument for anything. That it is little more than a haphazard collection of claims, that are not only not supported by evidence, but do not even form a consistent sequence.
All references are to the paperback 2020 edition.
Preamble
The most striking feature of the book before us is that it is difficult to find a way to approach it. A sociological study and a political pamphlet still have something in common: they have a goal. The goal is to convince the reader. The methods of convincing can be quite different, involve data and logic and authority. But in any case, something is needed. As you start reading Feminism Interrupted you are bound to find that this something is hidden very well. Indeed, as I just counted, one of the first sections Who’s the boss has as many claims as it has sentences (some claims are in the form of rhetorical questions). There, as you see, was no space left for any form of supporting argumentation. Because it is not immediately obvious how to analyse a text with such a (non-)structure, let me start the same way as Ms. Olufemi starts in Introduction and just read along, jotting down notes and impressions, gradually finding our way through the book, forming a conception of the whole.
The following is a numbered list of places in the book that made me sigh or laugh. They are classified as: E (not supported by Evidence), C (Contradiction with itself or an earlier claim) and I (Incoherence). These classes are necessarily arbitrary and overlapping. I will also provide a commentary about some common themes and undercurrents running through the book.
One may object that this is too pedantic a way to review a book. Well, maybe it is, but this is the only way I know to lay ground for justifiable conclusions, with which my review will be concluded.
Notes on the text
1.E, p. 4: “neo-liberalism refers to the imposition of cultural and economic policies and practices by NGOs and governments in the last three to four decades that have resulted in the extraction and redistribution of public resources from the working class upwards “ — this of course has very little to do with the definition of Neo-liberalism. Trivial as it is, this sentence introduces one of the most interesting and unexpected themes that will resurface again and again: Ms. Olufemi, a self-anointed radical feminist from the extreme left of the political spectrum, in many respects is virtually indistinguishable from her brethren on the opposite side. Insidious “NGOs” machinating together with governments against common people are the staple imagery of the far-right.
2.C, p. 5: “… that feminism has a purpose beyond just highlighting the ways women are ‘discriminated’ against… It taught me that feminism’s task is to remedy the consequences of gendered oppression through organising… For me, ‘justice work’ involves reimagining the world we live in and working towards a liberated future for all… We refuse to remain silent about how our lives are limited by heterosexist, racist, capitalist patriarchy. We invest in a political education that seeks above all, to make injustice impossible to ignore. “ — With a characteristic ease, that we will appreciate to enjoy, Ms. Olufemi tells us that feminism is not words, and in the very next sentence, supports this by her refusal to remain silent.
3.C, p. 7: “Pop culture and mainstream narratives can democratise feminist theory, remove it from the realm of the academic and shine a light on important grassroots struggle, reminding us that feminism belongs to no one. “ —- Right after being schooled on how the iron fist of capitalist patriarchy controls every aspect of society, we suddenly learn that the capitalist society media welcomes the revolution.
4.C, p. 8: This is the first time that Ms. Olufemi has decided to cite a source (an article from Sp!ked, 2018). The reference is in the form of a footnote, and the footnote is a 70-character URL. That is what almost all her references and footnotes look like. A particularly gorgeous URL is in footnote 3 on p. 53: it’s 173 characters, of which the last 70 are unreadable gibberish. Am I supposed to retype this character-by-character on my phone? Or the references are for ornamentation only? In any case, it seems Ms. Olufemi either cannot hide her extreme contempt for the readers, or spent her life among people with an unusual amount of leisure.
5.E, p. 15: “When black feminists […] organised in the UK […] [t]hey were working towards collective improvement in material conditions… For example…” — The examples provided are: Grunwick strike by South Asian women and an Indian lady, Jayaben Desai. Right in the next sentence after that, Ms. Olufemi concludes: “There is a long history of black women […] mounting organised and strategic campaigning and lobbying efforts“. Again as in 2.C, she is completely unabated by the fact that the best examples of black feminist activities that she is able to furnish, have nothing to do with black feminists.
6.E. p. 23: “Critical feminism argues that state sexism has not lessened [for the last 50 years]“. Evidence: “MPs in parliament hide the very insidious ways that the state continues to enable male dominance … “ —- tension rises! — “the Conservative government introduced their plans to pass a Domestic Violence Bill with the intention of increasing the number of convictions for perpetrators of abuse…. “ — which looks good on the surface, but of course — “it is simply another example of the way the state plays on our anxieties about women’s oppression to disguise the enactment of policies that trap women in subordinate positions.” — Finally, we are about to learn how exactly the governments (and NGOs, remember!) keep women subjugated for the last 50 years, we are agog with curiosity! — “Research from the Prison Reform Trust has found an increase in the number of survivors being arrested” (p. 24) — And then… And then there is nothing. How does this prove that things are not better than 50 years ago? Just follow Mr. Olufemi example, and completely expunge from your mind everything that you claimed more than five sentences and seconds ago.
7.C, p. 26. “But this figure does not tell the whole story. The impact of these cuts is felt particularly by low-income black women and women of colour. “ — Another constant motif of the book is that Ms. Olufemi alternately blames the state for violence and overreach, only to immediately request expansion of paternalistic services and welfare.
8.C, p. 27: “If a woman must disclose […] that she has been raped […] her dignity, agency and power over personal information is compromised. “ — In a sudden turn of events our feminist seems to argue that it would be preferable for rape survivors to stay silent.
9.E, p. 28: When she does provide any sort of supporting evidence, it feels better that she wouldn’t: “We know that thousands of disabled people have died as a direct result of government negligence surrounding Personal Independence Payments […]9“ — The footnote is nothing but a 100 character URL, that I patiently typed in, only to be greeted with 404. According to webarchive.org, the referred-to page never existed. Ultimately, after many false starts (whose details I shall spare you), I found the document at a completely different web-site: https://questions-statements.parliament.uk/written-questions/detail/2018-12-19/203817 . Imagine my (lack of) surprise, when it turned out that government “negligence” is neither mentioned nor in any way implied or imputed—Ms. Olufemi simply fabricated the whole story.
10.I, p.29: “[In Yarl’s Wood IRC] they are locked in, unable to leave and subjected to surveillance by outsourced security guards. Tucked away in Bedford outside of the public consciousness, it’s hard to think of a more potent example of state violence.” — Judgment of anybody who, in the world of wars, continuous genocides and slaughter of human beings, maintains that the worst example of state violence is the sufferings of the women, who fled their ruined countries to the relative safety of the UK, must be thoroughly questioned. The second quoted sentence is also indefensible grammatically.
11.E, p. 30: In support of her claim that the state violently oppresses black women, Ms. Olufemi provides stories of 3 black women, that died in police custody over the course of… 50 years. “they reveal a pattern“ — she confidently concludes. No, they don’t. Statistical data would, but they do not support Ms. Olufemi’s thesis. She then proceeds to lament “a dystopian nightmare for the undocumented migrants“ — conveniently forgetting that these people tried as hard as they could to move to the dystopian UK and none of them hurried back. The section the quote is from is called State Killings — the 3 examples provided are somehow put in the same rubric as the doings of Pol-Pot and Mao.
12.E, p. 31: “If black women die disproportionately at the hands of the police, historically and in the present moment” — and then she proceeds on the assumption that they do, without providing any evidence. Immediately available public data (from INQUEST and IOPC reports), clearly refute the premise.
13.C, p. 32: “This refusal to participate [in capitalism] takes many forms: feminist activists are finding new and creative ways to oppose austerity.“ — Ms. Olufemi’s personal creative way to refuse to participate in the capitalist economy is to copyright a book, publish it with a publishing corporation (a capitalist enterprise, mind you) and then collect the royalties.
14.E., p. 33: “Sisters Uncut has put domestic and sexual violence on the national agenda” — Ms. Olufemi’s desire to prop her friends is laudable, but it does not eliminate the need to provide evidence.
15.I., p.33: “When I ask Sandy where the idea to create Sisters came from, she tells me” — Who’s Sandy? No Sandy was mentioned before. A certain Sandy Stone, the author of A Posttranssexual Manifesto appears 30 pages later, but it is unlikely she is meant here. The simple present tense of the sentence uncannily reminds of the way children talk about their imaginary friends.
16.C., p. 36: “So that just […] – Shulamith Firestone” — Oops, Ms. Olufemi approvingly quotes S. Firestone — a central figure in the so much derided second-wave liberal feminism.
17.C, p. 38: Trying to tie ‘social reproduction’ to race, Ms. Olufemi notices: “Wealthy white women have always been able to exercise greater agency over their reproductive capacity because they can afford private healthcare and specialist medical advice “, omitting to mention that so have wealthy black women too. The difference, as she herself emphasised with the “because” part, is in wealth not race. Mr. Olufemi then proceeds to build far-reaching conclusions from this rather trivial error.
18.E, p. 39: Being a radical revolutionary, Ms. Olufemi is not afraid to cast aspersions on defenceless dead women: “Margaret Sanger, reproductive rights advocate responsible for the first birth control-clinic in the United States was a vocal eugenicist“ — the consensus in the literature is that M. Sanger was not a eugenist or racist in any shape of form. See
- Roberts, Dorothy (1998). Killing the Black Body: Race, Reproduction, and the Meaning of Liberty. Knopf Doubleday. ISBN 9780679758693. LCCN 97002383, p.77--78
- Gordon, Linda (2002). The Moral Property of Women: A History of Birth Control Politics in America. University of Illinois Press. ISBN 9780252027642.
- Valenza, Charles (1985). "Was Margaret Sanger a Racist?". Family Planning Perspectives. 17 (1). Guttmacher Institute: 44–46. doi:10.2307/2135230. JSTOR 2135230. PMID 3884362
Ms. Olufemi’s source? Angela Davis. At this point, let me make an aside. Ms Olufemi treats Angela Davis as a kind of mother figure and a hero: she quotes her left and right, and puts her on the blurb of the back cover. Angela Davis, in the meantime, is a KGB stooge, a “useful idiot” in an apt expression of Lenin. That beacon of freedom-fighting unashamedly praised and was on the pay of the Soviet communist regime that, as was very well-known at the time, organised the extermination of tens of millions of people.
19.C, p. 41: Suddenly Ms. Olufemi lashes out against contraceptives, linking them to… eugenic: “eugenics has shaped our notion of family […] the racist logic of ‘population control’ that birthed the desire for contraceptives” — in this place again, it’s difficult to tell her from far-right and religious fundamentalists.
20.C, p. 44: “nobody understands the stakes around the right to access abortion and reproductive justice more than working class women“ — That looks like a good point to discuss Ms. Olufemi’s background. Far from being qualified to understand the “stakes”, she comes from what definitely does not look like a working class: after graduating from a privileged grammar school, she was immediately forced by the oppressive patriarchal society to study at Cambridge. Her PhD. research was sponsored (via TECHNE AHRC) by the very same government that she so mercilessly scrutinises in the present opus.
21.E, p. 44: “Ireland is coded ‘white’, and ‘Irish woman’ means only those who fall under that coding“ — neither of these claims is supported. Fortunately they are, as usual, in no way used in the following, because Ms Olufemi quickly switches to other, equally unsupported, claims.
22.E, p. 47: “English MPs voted […] to change Northern Ireland’s abortion law […]. This means that Abortion in Northern Ireland has only recently been decriminalised, the possibility of persecution has been lifted from those administering and undergoing abortions. “ — (Capitalisation as in the original.) There were no “underground” abortions in N. Ireland, because free abortions were available in England, a few hours away on a ferry.
23.E, p. 47: “The tendency to consider the UK a progressive environment for reproductive justice sorely underestimates the number of people, who despite the change in law may still have no recourse to abortion services“ — Well, then tell us.
24.E, p. 48: “Winning radically would mean […] a world without work” — That’s refreshingly honest, even though Marx won’t approve of such blatant revisionism.
25.E, p. 50: “throughout history, to be ‘female’ has often meant death, mutilation and oppression” — this unsupported claim is clearly wrong. Throughout history, most victims of violence by a large margin were and are men. Most people killed in the wars are men. Most people dying a violent death are men. Most people in prisons and mental institutions are men. More than 90% of work-related deaths happen to men.
26.I, p. 50: “If there are only two categories, it is easier for us to organise the world and attach feelings, emotions and ways of being to each one.“ — If it were so, then all categories would have been binary: there would have been 2 nations, 2 fashion styles, etc.
27.C, p. 50 Ms. Olufemi continues to argue that gender is fluid and a person can change it at will. Her arguments: “there is no way to adequately describe what gender is. Every definition does a disservice to the shifting, multiple and complex set of power relations that come to shape a person’s gender.“ — It would be interesting to trace her train of thought if “gender” were replaced with “race” in this sentence. As race is much more of a social construct and less rooted in biology, surely Ms. Olufemi would agree that we should welcome when a “racially dysphoric” white person claims to be black. Unfortunately that would uproot her basic tenet about the exclusivity of black women’s experience and its central role in the formation of radical feminism.
28.C, p. 52: “If one group of people consistently behave, speak, move, present themselves in one way and another in the ‘opposite’ way, we reaffirm the idea that there is actually an inherent difference between those two groups when no such difference exists.“ — I guess the groups Ms. Olufemi has in mind are males and females. Or maybe whites and blacks?
29.C, p. 52: “Many intersex infants […] have surgery to ‘correct’ their genitalia without their consent.“ — That’s an interesting notion. Should we abstain from, for example, fixing broken bones of small children, until such time as they would be mature enough to consent?
30.E, p. 53: “Many women are physically stronger than men; many men are physically weaker than women. These are not exceptions that defy a rule; there simply is no rule.” — This betrays an utter ignorance of statistics and data. Normal distribution of strength (as measured, for example, by grip tests) in a population with different means for males and females is among the most reliably established anthropometrical facts.
31.E, p. 54: “To argue that there is a clear difference between sex and gender serves to solidify the idea that biological sex, prior to human beings inventing it and naming its tenants, exists.“ — here again Ms. Olufemi joins far-right and religious fundamentalists in her anti-science stance and denial of the evolutionary origin of mechanisms of sexual reproduction. The objective existence of biological sex, manifested in morphological, physiological and behavioural differences (sexual dimorphism) is attested beyond the slightest doubt across the entire animal kingdom.
32.E, p.68: “It is the public rejoicing at 19-year-old Shamima Begum being stripped of her citizenship “ — Ms. Olufemi chose as her example of Islamophobia a girl who joined ISIS, and became there an enforcer that threatened other women with death lest they comply with ISIS rules, stripped suicide vests into their clothes and ended up burying all her 3 children in this non-secular utopia.
33.E, p. 71: “Muslim women are the most economically disenfranchised group in the country.” — this simple claim is simply wrong. According to the UK Office for National Statistics, the most economically disenfranchised group in the UK are (as expected) refugees and asylum seekers, followed (unfortunately for Ms. Olufemi) by white workers in “post-industrial” (read: de-industrialised) communities.
34.C, p. 74: “A staunchly secular way of thinking about our lives and bodies limits Muslim women’s ability to understand themselves “ — Ms. Olufemi sympathy for organised monotheistic religions and her distrust in the secular society is rather unexpected. It is not clear how to reconcile her idea that to better understand themselves women should abandon secularism and return to the church or mosque with the feminist dogma.
35.I, p. 76: “creation of a public outcry about ‘Asian Grooming Gangs.’” — It’s sad that a feminist can scary-quote and dismiss one of the most horrible cases of mass abuse of women. A sacrifice of the suffering of more than a thousand girls to make a vindictive political point does not paint Ms. Olufemi as a good human being.
36.I, p. 86: “Art is a tool for feminist propaganda “ — Unfortunately Ms. Olufemi forgot that this chapter is called Art for Art’s Sake and its main thesis is that art of not a tool of anything. Notice also how she repeats Stalin and Goebbels almost verbatim.
37.C, p. 88: “Poor women do not get to make art: the fact that Saye’s work could be displayed in one of the most prestigious arenas in the world … calls us to wake up to the cruelty of inequity. ” — This is probably one of the most impressive examples of Ms. Olufemi’s ability to forget the beginning of a sentence (that she wrote!) by the time she gets to its middle — she demonstrates that poor women cannot make art by an example of a poor woman whose art became fashionable and famous. But then she easily outdoes herself! By the time we get to the end of the sentence, she forgets what was in the middle (or otherwise she thinks that being displayed at a Venice Biennale is unusually cruel).
38.C, p. 89: “Momtaza Mehri, essayist, researcher and former Poet Laureate for young people, tells me. ” — Ms. Olufemi continues to give proof of art being unavailable to poor women by providing another example: of a poor woman who was a Poet Laureate.
39.I, p. 110: “The idea that justice is served when criminals go to prison is relatively new. […] Ironically, prisons were introduced in order to make punishment more ‘humane’.” — Unironically, this is one of the most blatantly ignorant statements to grace the printing press lately. Prisons, as known to anybody with even superficial knowledge of history, existed as long as states did. There are some echoes of Foucault in that sentence, but poorly read or remembered, because his conclusion was the opposite.
40.E, p. 123: “In July 2019, Cancer Research UK, fundraising partners with dieting organisation Slimming World, launched a multi-million pound campaign using defunct scientific indicators to claim that obesity was the second leading cause of cancer. “ — This is outright dangerous. Spreading falsehoods to the vulnerable people in the risk groups is extremely irresponsible. Large‑scale cohort studies show that higher body mass index (BMI) and excess adiposity correlate with increased incidence and worse outcomes for multiple cancer types. These data form the backbone of public‑health recommendations promoting weight management:
- Renehan AG, Tyson M, Egger M, Heller RF, Zwahlen M. “Body-mass index and incidence of cancer: a systematic review and meta-analysis of prospective observational studies.” The Lancet, 371(9612), 569-578 (2008).
- Bhaskaran K, Douglas I, Forbes H, dos-Santos-Silva I, Leon DA, Smeeth L. “Body-mass index and risk of 22 specific cancers: a population-based cohort study of 5·24 million UK adults.” The Lancet, 384(9945), 755-765 (2014).
41.I, p. 124: “There is no clearer manifestation of neo-liberalism than in our attitudes towards bodies. “ — this, in the words of Pauli “is not even wrong”, whatever “attitudes toward bodies” means, they are not the clearest manifestation of neo-liberalism.
42.C, p. 125: “the myth that fatness means ill health” — Again, Ms Olufemi would be home with far-right conspiracy theorists. Excess adipose tissue (body fat) is strongly linked to a variety of health problems, including hypertension, insulin resistance, type 2 diabetes, cardiovascular disease, sleep apnea, and certain cancers. Medical researchers generally treat obesity as a risk factor that actively contributes to many of these conditions.
43.I, p. 126: “Nearly half of single parents in the UK – working or unemployed – live in relative poverty. “ — That’s because relative poverty is defined by the UK statistical agencies as “being poorer than half of the population”.
At this point your humble Scheherazade broke off in exhaustion.
Conclusions
“we need to remove the shame in the way we talk about acceptable forms of killing” — p. 48
I hope my notes demonstrated that even the most lenient and indulgent reader would quickly conclude that Feminism Interrupted is balderdash. That would be, however, too trivial a conclusion. Everything has a purpose and Ms. Olufemi book can find one with our help. As far as I can see, the purpose is to realise that even though incoherent and rambling, the text has a texture, some recurrent images appear again and again:
1. Ms Olufemi continuously laments the exploitation, poverty and oppression of women in the UK. Well, as everything in human condition, exploitation is relative. Ms. Olufemi enjoys the life of comfort, privilege and ease unimaginable to anyone outside of the scopes of the "developed" (i.e., capitalist) world or the last hundred years. She imagines a utopia of a stateless society free of "exploitation", but there is no indication that this eschaton is possible. It is not even a practical possibility that is questionable, but logical: is her image free of internal contradictions? All attempts to realise this millenialist dream, from Bogomils to Soviet and Chinese communists, are remembered for little besides industrial scale murder they invariably resulted in.
2. Ms. Olufemi’s feelings toward organised religion are clearly ambiguous. On one hand, she presumably understands that organised religion is the core institution of patriarchy that maintains and perpetuates values and structures that she finds so odious. On the other hand, she obviously cannot stop expressing her admiration of the austere faith of Mohammed, comparing it favourably with the decadent secular societies of the West.
3. Ms. Olufemi cannot decide whether she wants to abolish the state or expand it tremendously. Often in the course of the same period she registers her conviction that the state is evil and should be abolished, only to proceed to point out how unjust it is that the state does not sufficiently help the dispossessed and to request enlargement of welfare.
4. As was noted on many occasions, many of Ms. Olufemi’s positions echo ones of far-right conspirologists. Her distrust of science and NGOs makes one reconsider the “horseshoe theory” favourably.
2025-03-03
Publish or Perish in style.
Joseph Liouville, a famous French mathematician, whom multiple important theorems are named after, was also the founder and the editor of Journal de Mathématiques Pures et Appliquées, universally known as Liouville's journal (still in print, still very prestigious, two centuries later!).
Here is the list of the articles Liouville published in his own journal in 1861:
And then some more:... and more ...
...Look somewhat... similar don't they? The truth is, Liouville proved a certain general result about quadratic forms, but chose to keep it secret. Instead, he published almost two hundred papers with special cases, easily obtainable from his general theorem, but rather mysterious otherwise.References
2025-02-25
Long [story of] division.
The following text can be viewed as extremely dry and intimidating, or, equally, lightheadedly funny.
Let's formally verify the venerable long-division algorithm.
uintN_t div(uintN_t n, uintN_t d) {
uintN_t q := 0;
uintN_t r := 0;
int i := N - 1;
while (i != -1) {
r <<= 1;
r |= ((n >> i) & 1);
if (r >= d) {
r := r - d;
q |= 1 << i;
}
i := i - 1;
}
return q;
}Here uintN_t is the type of unsigned N-bit integers, N > 0.
We shall establish formal correctness via Hoare logic. The following is by no means an introduction to the subject, our presentation skims over a large number of important details, please refer to the literature cited on the Wikipedia page. The basic element of Hoare logic is a Hoare triple, which is a construction of the form
⟦ precondition ⟧ COMMAND ⟦ postcondition ⟧
This triple means that if an execution of COMMAND starts in a state satisfying precondition, then the execution can only terminate in a state satisfying postcondition. (We use ⟦ and ⟧ instead of more traditional { and }, because our ambient language uses braces.) The pre- and postconditions are formulae of predicate calculus that can refer to the terms of the programming language (variables, literals, etc.). A triple is valid, if it can be proved starting from the usual rules of the predicate calculus and certain axioms. For a given programming language, one presents a list of axioms, describing the behaviour of the language constructs, and then proves soundness, i.e., establishes that the axioms and the accepted rules of inference are satisfied by all possible computations. We will need the following axioms:
Axiom of assignment
⟦ S[ x := E ] ⟧ x := E ⟦ S ⟧
Here S[ x:= E ] is the result of substituting E for each occurrence of x in the formula S. (In this form the axiom really only works for simple unaliased variables and does not work for pointers or arrays, which is sufficient in our case.) The axiom looks "backward", so let's play with it a bit. First, check that the assignment does set the variable to the desired value:
⟦ ? ⟧ x := 4 ⟦ x == 4 ⟧
The command is a simple assignment x := 4, the postcondition, x == 4, verifies that the variable got the expected value. What precondition guarantees that the assignment establishes the postcondition? The assignment axiom gives us for the precondition (x == 4)[ x := 4 ] = (4 == 4) = true. That is, no matter what was going on before the assignment, after it terminates, x == 4, as expected:
⟦ true ⟧ x := 4 ⟦ x == 4 ⟧
A bit more complex example:
⟦ ? ⟧ x := x + 1 ⟦ x > 0 ⟧
What precondition guarantees that x will be positive after increment? We can compute the precondition, it is (x > 0)[ x := x + 1 ] = (x + 1 > 0) = (x > -1) — perfectly reasonable.
What if we are given a precondition does not have the form that the axiom requires?
⟦ x == A ⟧ x := x + d ⟦ ? ⟧
S, such that (x == A) = S[ x := x + d ]
Well, in this case you are stuck. To derive a postcondition using the axiom of assignment, you first have to massage the precondition in a form, where x only happens as part of E. Fortunately in this case it's easy:
/* Comments as in PL/I. */ ⟦ x == A ⟧ /* Simple arithmetics: add d to both sides. */ ⟦ x + d == A + d ⟧ x := x + d ⟦ x == A + d ⟧
What if the precondition does not contain x? Then the assignment is useless for program correctness, and, hence, can be most likely discarded. :-)
Typically, when you use the assignment axiom for a formal verification, you have to come up with a precondition, that has one or more instances of E and then the axiom let's you to jump to a postcondition where each E is simplified to x.
Next is
Axiom of composition
This axiom describes the ;-sequencing operator.
If we have
⟦ precondition ⟧ COMMAND0 ⟦ condition ⟧
and
⟦ condition ⟧ COMMAND1 ⟦ postcondition ⟧
Then the axiom allows us to conclude
⟦ precondition ⟧ COMMAND0 ; COMMAND1 ⟦ postcondition ⟧
This matches the expected semantics of sequential execution.
Conditional axiom
For a conditional statement of a form
if (guard) {
COMMAND0
} else {
COMMAND1
}We have
⟦ precondition ⟧ if (guard) { ⟦ guard && precondition ⟧ COMMAND0; ⟦ postcondition ⟧ } else { ⟦ !guard && precondition ⟧ COMMAND0; ⟦ postcondition ⟧ } ⟦ postcondition ⟧
That is, if both "then" and "else" commands establish the same postcondition, given the original precondition strengthened by the guard or its negation, then the entire conditional statement establishes the same postcondition. This is fairly intuitively obvious.
Finally, we need
While-loop axiom
Consider a loop
while (guard) {
BODY
}To apply the while-loop axiom, we have to find an assertion, called a loop invariant that is preserved by the loop body, that is such that
⟦ guard && invariant ⟧ BODY ⟦ invariant ⟧
If the body is entered, while the invariant holds (and the guard holds too), then the invariant is true at the end of the body execution. Given an invariant, the while-loop axiom gives
⟦ invariant ⟧ while (guard) { BODY } ⟦ !guard && invariant ⟧
In other words, if the invariant was true at the beginning of the loop execution, then it is true when the loop terminates. The while-loop axiom shows to an observant reader that loops are pure magic: it is the only construction that starts in a state satisfying a known condition, given by the invariant, and then miraculously strengthens that condition by adding !guard conjunct. Perhaps due to this the founders of structured programming preferred while-loops to the much-derided loops with "a control variable", like DO loops in FORTRAN and for-each loops of the modern languages.
There are many more axioms (what about the rules for function calls and recursion?), but we won't need them or will hand-wave around them.
Now, back to the long division. We want to establish the validity of the following triple:
uintN_t div(uintN_t n, uintN_t d) {
⟦ d > 0 ⟧
uintN_t q := 0;
uintN_t r := 0;
int i := N - 1;
while (i != -1) {
r <<= 1;
r |= ((n >> i) & 1);
if (r >= d) {
r := r - d;
q |= 1 << i;
}
i := i - 1;
}
⟦ n == d*q + r && 0 <= r && r < d ⟧
return q;
}The structure of the code basically forces the structure of any possible proof:
- Find an invariant, preserved by the loop body.
- Prove that the invariant is established before the loop is entered.
- Prove that the desired postcondition follows from the conjunction of the invariant and the negation of the guard.
Finding a suitable invariant is the most non-trivial part of the job. Fortunately, in this case we are helped by our (presumed) experience of manually executing this algorithm all too many times at the elementary school. To make it less boring, I give an example of how long division is done in my native country, you should be able to figure it out:
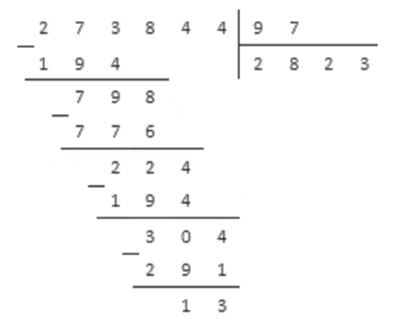
After the first step (when the subtraction under the first horizontal line on the left has been completed), the algorithm established that 273 == 97*2 + 79, where by construction 79 < 97, which looks promisingly similar to the form of the postcondition that we want to establish: n == d*q + r && r < d. It then makes sense to select as the invariant "the highest N - i - 1 digits of dividend (n), divided by the divisor (d), have the highest N - i - 1 digits of q as the quotient and r at the remainder" (in our binary case the digits are bits).
Provided that we manage to establish that this is actually an invariant, the other remaining pieces fall in place quickly:
- At the beginning of the loop,
i == N - 1so "the highestN - i - 1bits" degenerate into "the highest 0 bits", for which the condition is vacuous. - Similarly at the termination of the loop we have
i == -1, soN - i - 1 == Nand we have the desired postcondition.
But before we embark on the actual proof, we have to introduce some terminology, to simplify the necessary formal manipulations.
We are operating on N-bit unsigned binary numbers. We shall refer to the more and less significant bits as "left" or "last" or "high" and "right" or "first" or "low" respectively, with the appropriate comparative and superlative forms and without, of course, making any assumptions about endianness. Bits are indexed 0 ... N - 1 from right to left (Thank you, Fibonacci, very clever! Not.).
We will do a lot of bit-shifting. Recall that for t >= 0, x >> t == floor(x/2^t) and x << t == x*2^t. Again, all values are unsigned, and so are shifts. Bitwise OR and AND are denoted as | and & as in C.
On a loop iteration with a particular value of i, we will be especially interested in shifts by i and i + 1 bits. Write
B' = (1 << i)for thei-th bit bitmask.B" = (1 << (i + 1))for the(i + 1)-st bit bitmask.t' = (t >> i), for the valuetshiftedibits right.t" = (t >> (i + 1)), for the valuetshiftedi + 1bits right.M(k) = (1 << k) - 1, for the bitmask of the firstkbits.
We treat ' and " as singular operators, binding tighter than any binary ones.
As a warm-up, prove the following
LEMMA x' == 2*x" + x'&1
(Once you rewrite 2*x" as (x >> (i + 1)) << 1, it should be trivial.)
"The highest N - i - 1 bits" of x mentioned in the informal invariant above can be obtained by discarding the remaining N - (N - i - 1) == i + 1 bits, and so are x >> (i + 1), or, as we luckily agreed, x". It makes sense to try n" == d*q" + r && r < d && 0 <= r as the invariant. This assertion is established at the loop entrance and guarantees the final postcondition after the loop termination. Unfortunately, it is *not* an invariant of our loop. To conclude this, observe that this assertion holds at the loop entrance even if the initial value of q is not 0. If it were an invariant, then initialising q to an arbitrary value would still produce a correct result, which is clearly not the case, because bits of q are only set (by q |= 1 << i) and never cleared, so in the final value of q all the bits set initially remain set.
As it turns out (after many a painful attempt), this is the only obstruction and once we add to the invariant a conjunct q&M(i + 1) == 0 stating that i + 1 lowest bits of q are 0, we obtain the desired invariant:
LOOP INVARIANT n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0
(If you want a good laugh and have some time to spare, paste div() code in a ChatGPT chat and ask various models what the loop invariant is.)
To the proof then. First, check that the invariant is established at the loop entrance that is, that the following triple is valid.
⟦ d > 0 ⟧ uintN_t q := 0; uintN_t r := 0; int i := N - 1; ⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 ⟧
Go from bottom to top, applying the assignment axiom and simplifying on each step. First, expand the invariant as
⟦ n >> (i + 1) == d*(q >> (i + 1)) + r && r < d && 0 <= r && q&((1 << (i + 1)) - 1) == 0 ⟧Now apply the assignment axiom (i.e., replace i with (N - 1))...
⟦ n >> ((N - 1) + 1) == d*(q >> ((N - 1) + 1)) + r && r < d && 0 <= r && q&((1 << ((N - 1) + 1)) - 1) == 0 ⟧ i := N - 1; ⟦ n >> (i + 1) == d*(q >> (i + 1)) + r && r < d && 0 <= r && q&((1 << (i + 1)) - 1) == 0 ⟧
... simplify, use x >> N == 0 for any N-bit value, and apply the assignment axiom again ...
⟦ 0 == d*0 + 0 && 0 < d && 0 <= 0 && (q & ~0) == 0 ⟧ r := 0 ⟦ 0 == d*0 + r && r < d && 0 <= r && (q & ~0) == 0 ⟧
... and one more time ...
⟦ 0 == 0 && 0 < d && (0 & ~0) == 0 ⟧ q := 0 ⟦ 0 == d*0 + 0 && 0 < d && 0 <= 0 && (q & ~0) == 0 ⟧
... which finally gives
⟦ 0 < d ⟧Which is exactly the given precondition. Voilà! Interestingly, it seems division by zero is impossible, because there is no suitable remainder.
Next, we need to prove that the invariant is preserved by the loop body. This is by far the most complex and inundating part of the proof. We want to establish the following triple (at this point let's expand the compound assignment operators and add a trivial else to the conditional so that it conforms to the form expected by our conditional axiom):
⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 && i != -1 ⟧ r := r << 1; r := r | ((n >> i) & 1); if (r >= d) { r := r - d; q := q | (1 << i); } else { } i := i - 1; ⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 ⟧
First, the guard i != -1 is only needed to guarantee that shifts by i and i + 1 bits make sense. It is not used for anything else and will not be mentioned again.
We can proceed as before: start at the bottom and apply the assignment axiom to work our way up:
⟦ n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0 ⟧ i := i - 1; ⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 ⟧
Note that after substituting i - 1 for i, x" nicely transforms into x'. But at this point we are stuck: we know the postcondition that the conditional operator must establish, but we have no idea what its suitable precondition is. Take a step back. We now have n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0, that we will call the target. The composition of two assignments and one conditional operator, starting from the loop invariant must establish the target. Write it down:
LOOP INVARIANT n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0
TARGET n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0
Comparing the loop invariant and the target, we see that transforming the former into the latter takes:
- Replacing
q"withq'. - Replacing
n"withn'. - Replacing
q&M(i + 1) == 0withq&M(i) == 0.
The last one is easy: if the first i + 1 bits of q are zero (this is what q&M(i + 1) == 0 means), then a fortiori so are its i first bits, so q&M(i) == 0.
As for replacing q" with q' and n" with n', we will do this via the lemma we stated (and you proved) earlier. We will now apply transformations to the loop invariant such that: (i) it will make it possible to apply the lemma and (ii) it will produce the result that will be a suitable precondition for the following assignments. The right-hand sides of the assignments are r <<= 1 (that is 2*r) and r | ((n >> i) & 1) (that is r | (n'&1)), so we will try to produce an assertion having sub-formulae of this form.
The starting invariant again:
⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 ⟧Multiply both sides of all conjuncts by 2. This produces terms such that the lemma and the assignment axiom for r := 2*r can be applied.
⟦ 2*n" == 2*d*q" + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 ⟧Immediately we can apply the lemma: 2*q" == q' - q'&1.
⟦ 2*n" == d*(q' - q'&1) + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 ⟧ q&M(i + 1) == 0 hence we can drop q'&1, as it is guaranteed to be 0.
⟦ 2*n" == d*q' + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 ⟧Amazing! We got rid of q" and this is even before the first statement of the loop body was executed. Continue...
Looking forward to r := r | n'&1, we see that we have no |-s in sight, so the assignment axiom cannot be applied directly. Intuitively, this should not be the problem, because after r is doubled, its lowest bit is zero, and so | to it is the same as +, and we have plenty of additions. To prove this it will be nice to have a conjunct r&1 == 0 at that point. But if such a conjunct is present, then before the r := 2*r assignment it looked (as per the assignment axiom) as (2*r)&1 == 0, which is always true, and so we can just as well insert it at this point!
⟦ 2*n" == d*q' + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 && (2*r)&1 == 0 ⟧More pressingly, to apply the assignment axiom to r := r | n'&1 we need n'&1 next to each r. To this end, observe that n'&1 is either 0 or 1, and so if 2*r < 2*d then 2*r + n'&1 < 2*d.
⟦ 2*n" == d*q' + 2*r && 2*r + n'&1 < 2*d && 0 <= 2*r && q&M(i + 1) == 0 && (2*r)&1 == 0 ⟧We are fully ready to apply the assignment axiom:
⟦ 2*n" == d*q' + 2*r && 2*r + n'&1 < 2*d && 0 <= 2*r && q&M(i + 1) == 0 && (2*r)&1 == 0 ⟧ r := 2*r ⟦ 2*n" == d*q' + r && r + n'&1 < 2*d && 0 <= r && q&M(i + 1) == 0 && r&1 == 0 ⟧
Apply the lemma: 2*n" == n' - n'&1
⟦ n' == d*q' + r + n'&1 && r + n'&1 < 2*d && 0 <= r && q&M(i + 1) == 0 && r&1 == 0 ⟧The next statement is the assignment r := r | n'&1. Thanks to r&1 == 0 conjunct, carefully prepared in advance, we know that we can replace r + n'&1 with r | n'&1 and apply the assignment axiom:
⟦ n' == d*q' + r + n'&1 && r + n'&1 < 2*d && 0 <= r && q&M(i + 1) == 0 && r&1 == 0 ⟧ ⟦ n' == d*q' + (r | n'&1) && (r | n'&1) < 2*d && 0 <= r && q&M(i + 1) == 0 && r&1 == 0 ⟧ r := r | n'&1 ⟦ n' == d*q' + r && r < 2*d && 0 <= r && q&M(i + 1) == 0 ⟧
One starts feeling at this point, that the steps of the derivation are practically forced by the form of the invariant. The appearance of r + n'&1 components in the assertion is a result of using the lemma to get rid of q" and n". In fact, it seems possible that the algorithm itself could have been derived ad initio, given the invariant. More about this at the end.
We found the mysterious precondition of the conditional statement. One relatively simple final step remains: we have to establish that both conditional branches, given this precondition, establish the target. Let's start with the r >= d branch. We need
⟦ n' == d*q' + r && r < 2*d && 0 <= r && q&M(i + 1) == 0 && r >= d ⟧ r := r - d; q := q | B' ⟦ n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0 ⟧
Experienced as we are at this point, we can easily transform the precondition to a form suitable for the next assignment (and also drop the redundant 0 <= r conjunct, implied by the conditional guard):
⟦ n' == d*q' + (r - d) + d && r - d < d && q&M(i + 1) == 0 && r - d >= 0 ⟧Apply the assignment axiom
⟦ n' == d*q' + (r - d) + d && r - d < d && q&M(i + 1) == 0 && r - d >= 0 ⟧ r := r - d ⟦ n' == d*q' + r + d && r < d && q&M(i + 1) == 0 && r >= 0 ⟧
Prepare for the q := q | B' assignment. To this end, we have to transform the last assertion to a form where q only happens as a part of q | B'. First, from q&M(i + 1) == 0 it follows that q | B' == q + B' (because i-th bit of q is zero). Next, do the easy part, q&M(i + 1) == 0: weaken it, as was discussed above, to q&M(i) == 0, then, use (B' | M(i)) == 0 (immediately from the definition of M(i)) to arrive at (q | B')&M(i) == 0.
Next, deal with d*q' + r + d.
d*q' + r + d
== d*(q' + 1) + r
== d*(q + B')' + r /* Convince yourself that (x >> i) + 1 == (x + (1 << i)) >> i */
== d*(q | B')' + r
Apply the assignment axiom
⟦ n' == d*(q | B')' + r && r < d && (q|B')&M(i) == 0 && r >= 0 ⟧ q := q | B' ⟦ n' == d*q' + r && r < d && q&M(i) == 0 && r >= 0 ⟧
Wait a second. This is exactly the target: n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0. We are done! What remains, is the trivial verification for the r < d conditional branch:
⟦ n' == d*q' + r && r < 2*d && 0 <= r && q&M(i + 1) == 0 && r < d ⟧ /* Algebra and weakening q&M(i + 1) == 0 to q&M(i) == 0 */ ⟦ n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0 ⟧
We are done with the verification of the loop invariant!
We now know that our loop invariant is indeed an invariant. The while-loop axiom then assures us that at the termination of the loop, the invariant will still hold, together with the negation of the guard:
⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 ⟧ while (i != -1) { r <<= 1; r |= ((n >> i) & 1); if (r >= d) { r := r - d; q |= 1 << i; } i := i - 1; } ⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 && i == -1 ⟧
OK, so substitute i == -1 to the invariant:
⟦ n" == d*q" + r && r < d && 0 <= r && q&M(i + 1) == 0 && i == -1 ⟧ ⟦ n == d*q + r && r < d && 0 <= r ⟧
Hallelujah!
Let's put it all together
uintN_t div(uintN_t n, uintN_t d) {
⟦ d > 0 ⟧
⟦ 0 == 0 && 0 < d && (0 & ~0) == 0 ⟧
uintN_t q := 0;
⟦ 0 == d*0 + 0 && 0 < d && 0 <= 0 && (q & ~0) == 0 ⟧
uintN_t r := 0;
⟦ 0 == d*0 + r && r < d && 0 <= r && (q & ~0) == 0 ⟧
int i := N - 1;
⟦ n" == d*q" + r && 0 <= r && r < d && q&M(i + 1) == 0 ⟧
while (i != -1) {
⟦ n" == d*q" + r && 0 <= r && r < d && q&M(i + 1) == 0 && i != -1 ⟧
⟦ 2*n" == 2*d*q" + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 ⟧
⟦ 2*n" == d*(q' - q'&1) + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 ⟧
⟦ 2*n" == d*q' + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 ⟧
⟦ 2*n" == d*q' + 2*r && 2*r < 2*d && 0 <= 2*r && q&M(i + 1) == 0 && (2*r)&1 == 0 ⟧
⟦ 2*n" == d*q' + 2*r && 2*r + n'&1 < 2*d && 0 <= 2*r && q&M(i + 1) == 0 && (2*r)&1 == 0 ⟧
r <<= 1;
⟦ 2*n" == d*q' + r && r + n'&1 < 2*d && 0 <= r && q&M(i + 1) == 0 && r&1 == 0 ⟧
⟦ n' == d*q' + r + n'&1 && r + n'&1 < 2*d && 0 <= r && q&M(i + 1) == 0 && r&1 == 0 ⟧
r |= ((n >> i) & 1);
⟦ n' == d*q' + r && r < 2*d && 0 <= r && q&M(i + 1) == 0 ⟧
if (r >= d) {
⟦ n' == d*q' + r && r < 2*d && 0 <= r && q&M(i + 1) == 0 && r >= d ⟧
⟦ n' == d*q' + r + d && r < d && q&M(i + 1) == 0 && r >= 0 ⟧
r := r - d;
⟦ n' == d*q' + r + d && r < d && q&M(i + 1) == 0 && r >= 0 ⟧
⟦ n' == d*(q | B')' + r && r < d && (q|B')&M(i) == 0 && r >= 0 ⟧
q |= 1 << i;
⟦ n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0 ⟧
} else {
⟦ n' == d*q' + r && r < 2*d && 0 <= r && q&M(i + 1) == 0 && r < d ⟧
⟦ n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0 ⟧
}
⟦ n' == d*q' + r && r < d && 0 <= r && q&M(i) == 0 ⟧
i := i - 1;
⟦ n" == d*q" + r && 0 <= r && r < d && q&M(i + 1) == 0 ⟧
}
⟦ n" == d*q" + r && 0 <= r && r < d && i == -1 ⟧
⟦ n == d*q + r && 0 <= r && r < d ⟧
return q;
}Seriously, the proof above looks at a first (and then any following) sight, as a random barrage of bizarre formal spasms in haphazard directions. It is practically impossible to construct such a sequence of assertions in a top-to-bottom fashion, unless one spends an unhealthy amount of time interacting with Hoare triples in dark alleys.
And this is why nobody is doing it this way (among humans that is, automated provers are only too happy to try insane numbers of possible dead-ends). Early on, a much better-structured approach, going in the opposite direction, starting from the known targets (postconditions) was developed, see Predicate transformer semantics, or better still, read A Discipline of Programming ("59683rd Edition" as the Amazon page mentions nonchalantly). Dijkstra also shared the opinion that the structure of the program and the postcondition are tightly locked to the extent that it is possible to derive a program, given its formal specification, see the amazing EWD1162.



